leetcode刷题笔记

1.两数之和。

获得技能：哈希表，c++容器MAP。

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        map<int,int> a;//提供一对一的hash
        vector<int> b(2,-1);//用来承载结果，初始化一个大小为2，值为-1的容器b
        for(int i=0;i<nums.size();i++)
        {
            if(a.count(target-nums[i])>0)
            {
                b[0]=a[target-nums[i]];
                b[1]=i;
                break;
            }
            a[nums[i]]=i;//反过来放入map中，用来获取结果下标
        }
        return b;
    };
};

2.链表逆转。（非 力扣 ）

1.迭代法

• 需要保存：
  • 1.当前节点上一节点
  • 2.当前节点下一节点

List Reverse( List L )
{    
    List first=NULL;
    List tmp;
    while(L!=NULL)      //	L为当前节点
    {
        tmp=L->Next;    //   tmp保存下一节点
        L->Next=first;    //   修改指向
        first=L;      //	保存当前节点
        L=tmp;        //	转到下一个节点
    }
    return first;      //  返回头结点（不是L,L循环结束后为空）
}

2.栈

• 两次循环即可

void translateLinklist(Linklist& L)
{
  stack<int> stk;//定义栈
  
  Linklist p = L->next;
  while (p)  //依次读取栈的内容，也就是第一步
  {
    stk.push(p->data);
    p = p->next;
  }

  p = L->next;
  while (p)   //依次出栈，更换链表中的数据，也就是第二步
  {
    p->data = stk.top();
    stk.pop();
    p = p->next;
  }
}

3.无重复字符的最长子串。

获得技能：队列，滑动窗口

​

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        if(s.size() == 0) return 0;
        
        unordered_set<char> lookup; //队列模板
        
        int maxStr = 0;
        int left = 0;
        for(int i = 0; i < s.size(); i++){
            while (lookup.find(s[i]) != lookup.end()){
                lookup.erase(s[left]);
                left ++;
            }
            maxStr = max(maxStr,i-left+1);
            lookup.insert(s[i]);
    }
        return maxStr;
        
    }
};

4.寻找两个正序数组的中位数。

​ 获得技能：二分查找。

​

​ 由于数列是有序的，其实我们完全可以一半儿一半儿的排除。假设我们要找第 k 个数，我们可以每次循环排除掉 k/2 个数。

public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int m = nums2.length;
        //因为数组是从索引0开始的，因此我们在这里必须+1，即索引(k+1)的数，才是第k个数。
        int left = (n + m + 1) / 2;
        int right = (n + m + 2) / 2;
        //将偶数和奇数的情况合并，如果是奇数，会求两次同样的 k
        return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;
    }
    private int getKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
        //因为索引和算数不同6-0=6，但是是有7个数的，因为end初始就是数组长度-1构成的。
        //最后len代表当前数组(也可能是经过递归排除后的数组)，符合当前条件的元素的个数
        int len1 = end1 - start1 + 1;
        int len2 = end2 - start2 + 1;
        //让 len1 的长度小于 len2，这样就能保证如果有数组空了，一定是 len1
        //就是如果len1长度小于len2，把getKth()中参数互换位置，即原来的len2就变成了len1，即len1，永远比len2小
        if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);
        //如果一个数组中没有了元素，那么即从剩余数组nums2的其实start2开始加k再-1.
        //因为k代表个数，而不是索引，那么从nums2后再找k个数，那个就是start2 + k-1索引处就行了。因为还包含nums2[start2]也是一个数。因为它在上次迭代时并没有被排除
        if (len1 == 0) return nums2[start2 + k - 1];

        //如果k=1，表明最接近中位数了，即两个数组中start索引处，谁的值小，中位数就是谁(start索引之前表示经过迭代已经被排出的不合格的元素，即数组没被抛弃的逻辑上的范围是nums[start]--->nums[end])。
        if (k == 1) return Math.min(nums1[start1], nums2[start2]);

        //为了防止数组长度小于 k/2,每次比较都会从当前数组所生长度和k/2作比较，取其中的小的(如果取大的，数组就会越界)
        //然后素组如果len1小于k / 2，表示数组经过下一次遍历就会到末尾，然后后面就会在那个剩余的数组中寻找中位数
        int i = start1 + Math.min(len1, k / 2) - 1;
        int j = start2 + Math.min(len2, k / 2) - 1;

        //如果nums1[i] > nums2[j]，表示nums2数组中包含j索引，之前的元素，逻辑上全部淘汰，即下次从J+1开始。
        //而k则变为k - (j - start2 + 1)，即减去逻辑上排出的元素的个数(要加1，因为索引相减，相对于实际排除的时要少一个的)
        if (nums1[i] > nums2[j]) {
            return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
        }
        else {
            return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));
        }
    }

5.最长回文子串

​ 给你一个字符串 s，找到 s 中最长的回文子串。如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

* 中心扩展

class Solution {
public:
    string longestPalindrome(string s) {
        int len=s.size();
        if(len==0||len==1)
            return s;
        int start=0;//记录回文子串起始位置
        int end=0;//记录回文子串终止位置
        int mlen=0;//记录最大回文子串的长度
        for(int i=0;i<len;i++)
        {
            int len1=expendaroundcenter(s,i,i);//一个元素为中心
            int len2=expendaroundcenter(s,i,i+1);//两个元素为中心
            mlen=max(max(len1,len2),mlen);
            if(mlen>end-start+1)
            {
                start=i-(mlen-1)/2;
                end=i+mlen/2;
            }
        }
        return s.substr(start,mlen);
        //该函数的意思是获取从start开始长度为mlen长度的字符串
    }
private:
    int expendaroundcenter(string s,int left,int right)
    //计算以left和right为中心的回文串长度
    {
        int L=left;
        int R=right;
        while(L>=0 && R<s.length() && s[R]==s[L])
        {
            L--;
            R++;
        }
        return R-L-1;
    }
};

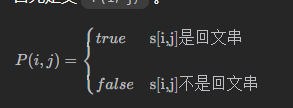
* 动态规划

​

​ 思想：如果S[ i , j ]是回文串，那么S[ i-1 , j -1]也是回文串 ， 假设

​ 需要注意 : i>j的情况

public String longestPalindrome(String s) {
    int length = s.length();
    boolean[][] P = new boolean[length][length];//公式
    int maxLen = 0;
    String maxPal = "";
    for (int len = 1; len <= length; len++) //遍历所有的长度
        for (int start = 0; start < length; start++) {
            int end = start + len - 1;
            if (end >= length) //下标已经越界，结束本次循环
                break;
            P[start][end] = (len == 1 || len == 2 || P[start + 1][end - 1]) && s.charAt(start) == s.charAt(end); //长度为 1 和 2 的单独判断下
            if (P[start][end] && len > maxLen) {
                maxPal = s.substring(start, end + 1);
            }
        }
    return maxPal;
}

6.约瑟夫环问题

1. 直接用数组实现

#include<bits/stdc++.h>
using namespace std;
//用数组实现约瑟夫环问题
int a[110]={0};   //元素值为0表示未出局 
//i既代表数组的下标，也代表每个人的编号
//k是用来计数的，一旦k的值达到m，代表此人需要出局，并且k需要重新计数，这样才能够找出所有需要出局的人
//数组的0代表未出局的人，数组非0代表出局的人，未出局的人需要报数，出局的人不需要报数 
int main()
{
  int N,M;
  int cnt=0,i=0,k=0;  //cnt表示目前出局的人数 
  cin>>N>>M;  //表示总共有n人，数到数字m时出局 
  while(cnt!=N) //因为要求N个人的出局顺序，因此当cnt（用来统计已经出局的人）未达到n时，需要循环不断报数 
  {
    i++;   //i是每个人的编号 
    if(i>N) i=1;  //这里需要特别注意：i的值是不断累加的，一旦发现i的值>N，那么i需要重新从第1个人开始
                  //数组要从第一个元素重新开始一个一个往后判断 
    if(a[i]==0)   //只有元素值为0的人 才需要报数，元素值为非0的代表已经出局了，不用报数 
    {
      k++;
      if(k==M)     //代表已经某个人已经报了M这个数，需要出局 
      {
        a[i]=1;  //编号为i的这个人出局 
        cnt++;   //出局的人数+1 
        cout<<i<<" ";  //输出出局的人的编号 
        k=0;   //清空k，让下一个人重新从1开始报数   
      }
    }
  }
  return 0;
} 

2. 循环链表

#include<bits/stdc++.h>
using namespace std;
//用链表实现约瑟夫环问题 （循环链表） 
 
typedef struct node  //typedef用来重命名struct node这种数据类型，将其命名为Node 
{
  int data;
  struct node* next;
}Node;
 
void ysflb(int N,int M)  //总共有N个人，报到数字为M的人出局 
{
  //初始化循环链表
  Node *head = NULL,*p=NULL,*r=NULL;   //head为头指针，指向链表的第一个结点，一开始赋值为NULL,代表不指向任何结点 
  head = (Node*)malloc(sizeof(Node));  //让head指向一个实际的空间
  if(NULL==head)  //内存空间可能会申请失败,大多数情况不会申请失败 
  {
      cout<<"Memory Failed!";
      return;
  } 
  head->data=1;       //从1开始编号 
  head->next=NULL;    //一开始整个链表只有一个Node(结点)，这个Node有两个域，分别是data和next
                      //data从1开始，next指向NULL，总共需要N个结点，现在创建了一个，还需要N-1个 
    p=head;             //head要保持不能改变，才能够找到链表的起始位置，一开始p也指向第一个结点
                      //p等一下会被使用，用它可以便于创建剩下的N-1个结点 
             
  //尾插法创建链表,已经有一个1号结点了，还需要创建剩下的n-1个结点 
  for(int i=2;i<=N;i++)
  {
    r=(Node*)malloc(sizeof(Node)); 
    r->data=i;
    r->next=NULL;
    //插入结点 
    p->next=r;
    p=r;
    
  }
  //创建循环链表
  p->next=head;   //最后一个结点的next指向头结点
  p=head;         //为后续方便，将p指向头结点
  
  //约瑟夫环的模拟
  while(p->next!= p)  //如果p的next=p，说明目前只有一个元素 
  {
    for(int i=1;i<M;i++)  //报到数字为M的时候出局 
    {
        r=p;   //保留出局的前一个结点 
        p=p->next; //p指向的是要出局的这个结点，需要保留前一个结点
    }
    // 输出
    cout<<p->data<<" ";
    r->next=p->next;    //删除p的目的，此时p指向哪里？  ：  
    p=p->next;  //更新p重新进行报数 
  } 
  cout<<p->data; 
}
 
int main()
{
  ysflb(10,3);
  return 0;
} 

7.列车调度问题

​ 建立一个数组，当输入一个列车序号时开辟轨道，再输入一个列车序号，在所有轨道中查找比列车序号大的列车序号，替换它，如果没有比它大的，则另开辟一个轨道。用top记录开辟轨道的数量。

#include<stdio.h>
int a[1000000];
int main()
{
  int n;
  scanf("%d",&n);
  int i,m,j,top=0;
  for(i=0;i<n;i++){
    scanf("%d",&m);
    if(top==0||a[top-1]<m){  //当top==0时，开辟轨道，当输入的列车序号比最上的轨道列车序号还大时，开辟轨道
      a[top++]=m;
    }else                   //二分查找
    { 
      int high=top-1,low=0,mid;
      while(low<=high)
      {
        mid=(low+high)/2;
        if(a[mid]>m)
        {
          high=mid-1;
        }else
        {
          low=mid+1;
        }
      }//a[mid]=m;
      a[low]=m;
    }
  }printf("%d",top);            //轨道数
}